코드네임 :
🖥️ 컴퓨터구조 - Memory! 본문
[ 지역성의 원칙 ]
: 프로그램은 어떤 특정시간에는 주소공간 내의 비교적 작은 부분만을 접근함
시간적 지역성
- 한번 참조된 항목은 곧바로 다시 참조되는 경향
- loop 내의 명령어, loop 내에서 반복적으로 업데이트 되는 변수

공간적 지역성
- 어떤 항목이 참조되면 그 근처에 있는 다른 항목들이 곧바로 참조될 가능성 높음
- 순차적 명령, 배열
ex)

메모리 계층구조 ⭐️


DRAM
- capacitor(콘덴서)에 전하로 저장
- DRAM의 메모리 셀 = 1개의 트랜지스터 + 1개의 capacitor
- capacitor는 비트값을 저장
- 주기적으로 refresh 필요
SRAM
- DRAM에 클럭 추가
- 메모리와 프로세서를 동기화하는 시간이 필요 X
DDR DRAM (Double Date Rate) : DDR4
- 대역폭 2배 향상
Flash Storage
비휘발성 반도체 저장장치
ㄴ 마모 균등화 필요
Disk Storage
비휘발성, 회전형 원판의 자기 저장장치
Disk Sectors and Disk Access
각 부문은 다음을 기록함
- Sector ID
- Data
- Error correcting code (ECC)
- Synchronizatoin fields and gaps


Cache Memory
작고 빠른 SRAM에 기반한 메모리로 hardware에 의한 관리
Cache vs Memory
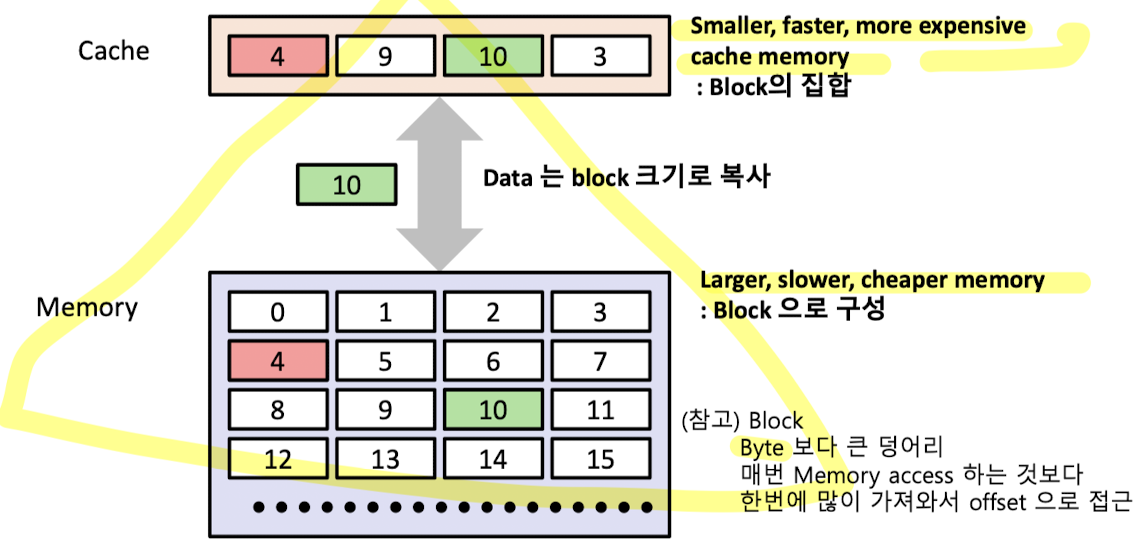
Cache의 Hit 와 Miss

Memory Design 법

[ Placement ]
Direct Mapped Cache

[Idenctification]

Direct Mapped Cache : 읽기
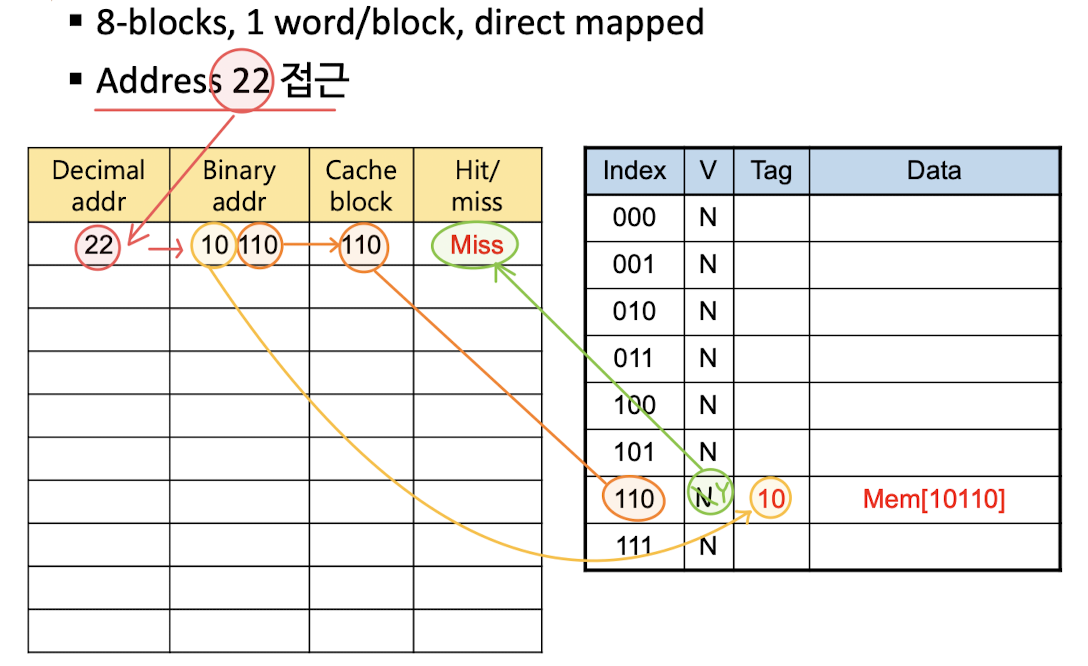

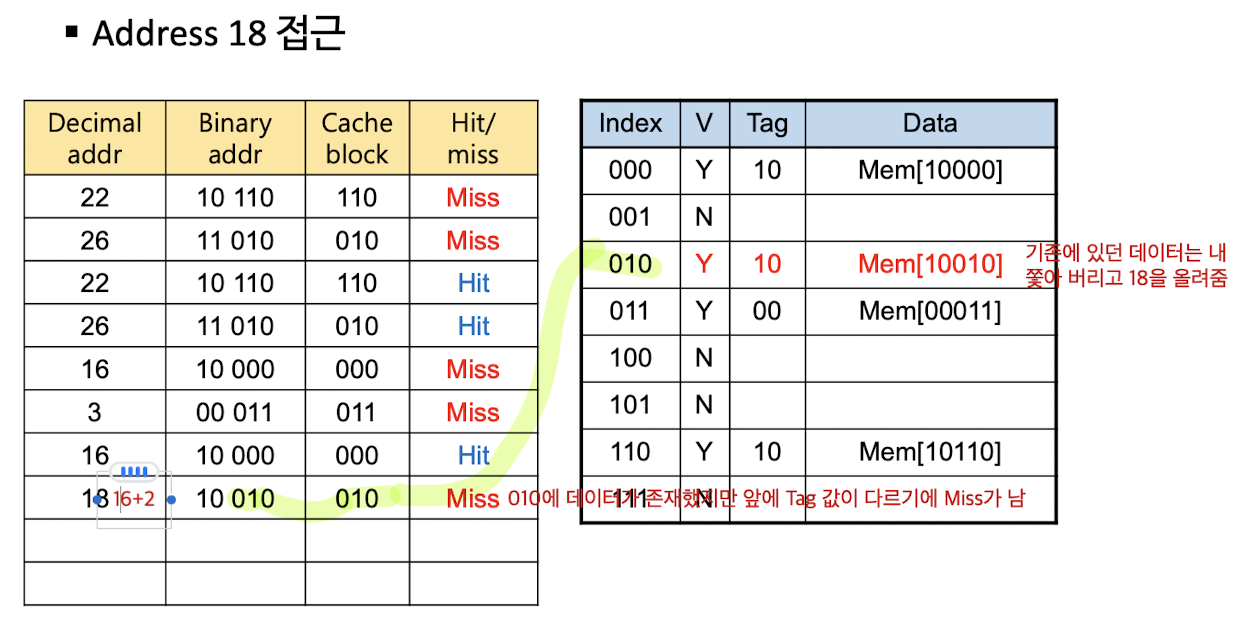
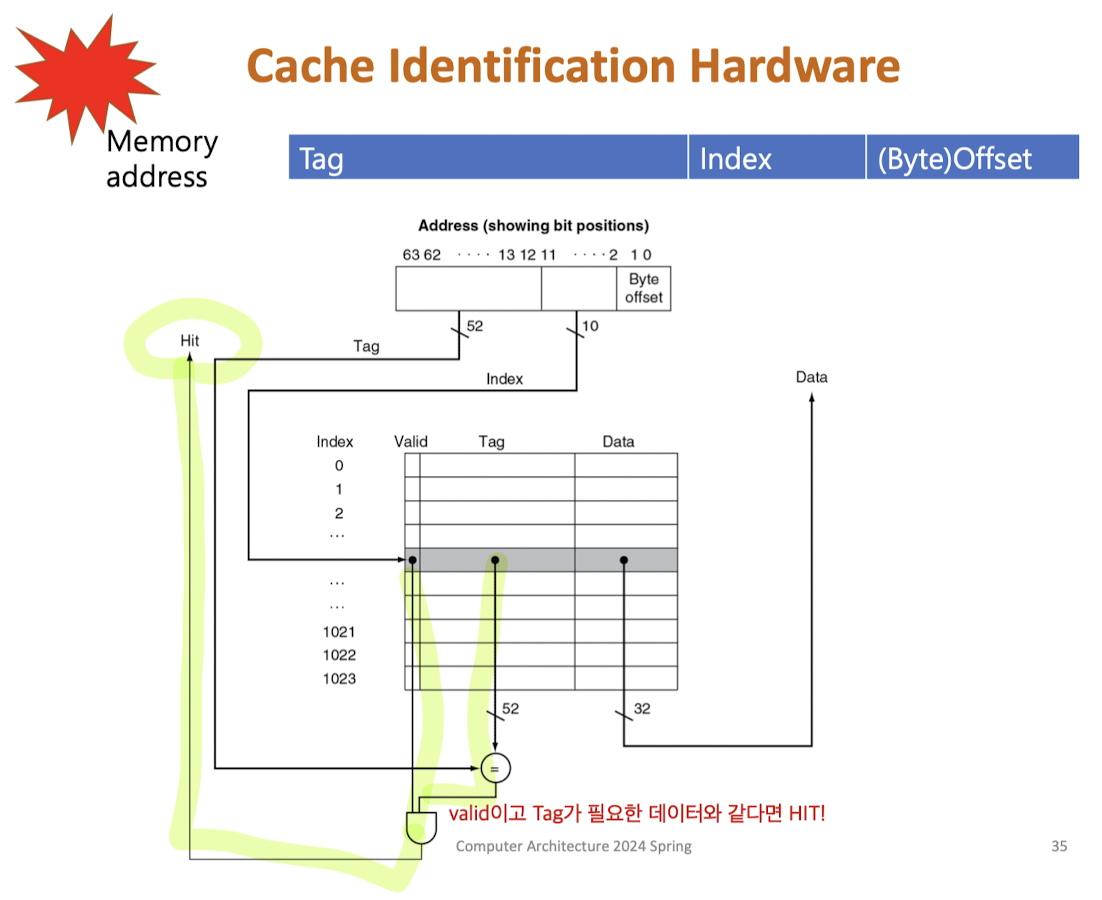
Write
: 레지스터에서 쫓겨날 때 쓰임
Write Through (즉시쓰기)

Write Back (나중 쓰기)

쓰기 할당

성능!!
1. CPU 성능이 향상되면,
Miss Penalty 의 중요성이 커짐 ( cache stall 영향이 큼 - 즉 cache miss )
2. CPI를 줄이면 (성능 향상)
메모리 stall 시간이 전체 실행 시잔 중에서 더 큰 부분을 차지
3. Clock rate (clock 속도) 만 향상 시키면
메모리 stall 시간이 전체 실행 시간 중에서 더 큰 부분을 차지
➡️ 시스템의 성능을 분석 시 cache의 영향 큼
[ Placement ] ⭐️
Fully associative (완전 연관)
- 블록이 캐시의 어느 곳에도 들어갈 수 있는 캐시 구조
- cache 내의 모든 엔트리 검색 필요 (캐시 엔트리)
- 모든 엔트리당 비교기 필요 (비용 증가)

n-way set associative (n-way 집합 연관)
- 각 블록이 들어갈 수 있는 장소의 개수가 n개로 정해져 있는 캐시 (적어도 2곳 이상)
(2-way set associative, 4-way, 8-way, ...)
- 각 set은 n개의 엔트리 구성 캐시 엔트리
- Block 주소에서 set을 결정
- set 내의 모든 엔트리 검색 필요
- n개의 엔트리당 비교기 필요 (비용 덜 증가)
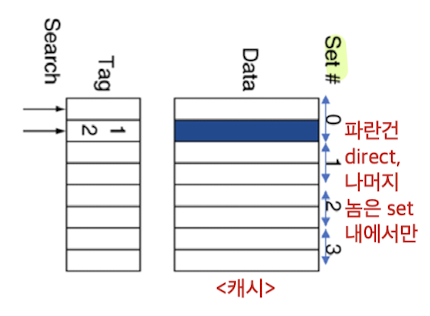
➡️ Fully 에서는 블록이 캐시 어느 곳에나 들어갈 수 있지만, n-way는 set내에서만 들어갈 수 있다
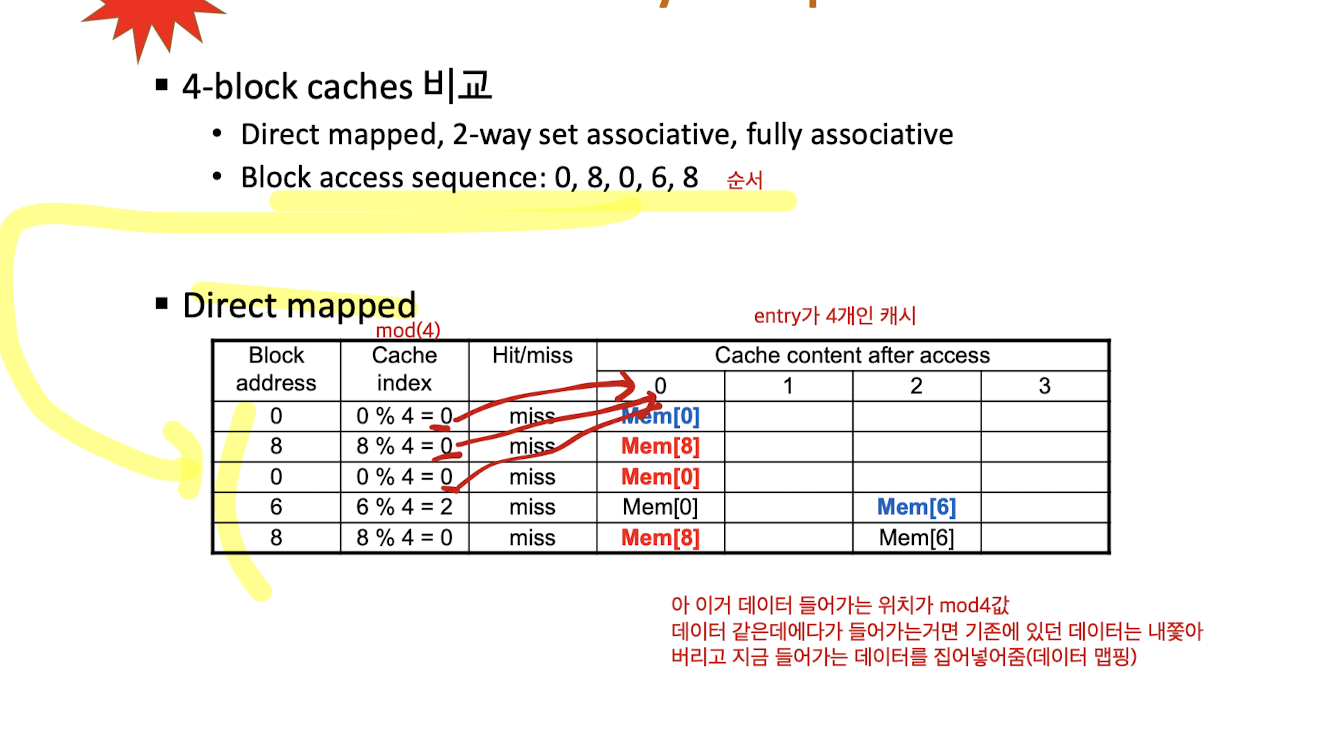

Associativity 를 증가시키면, miss rate는 감소됨
- 무작정 증가시킨다고, 계속 감소되는 거는 아님
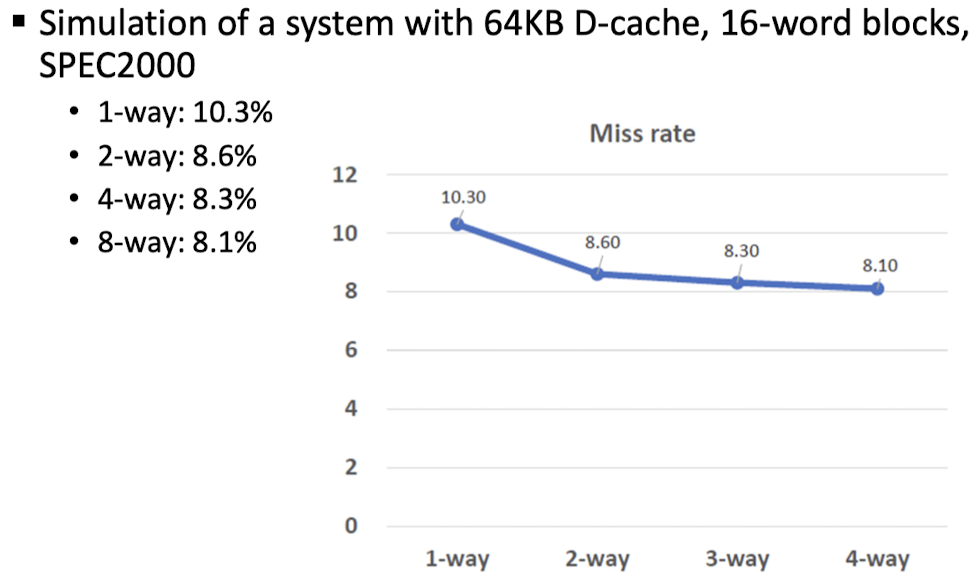
[ Replacement Policy (교체할 블록의 선택) ]
1. Direct mapped의 경우
- 그냥 교체 (내쫓김)
2. Set associative의 경우
- non-valid가 딱 1개 있다면 그거 비워버리고 거기에다가 데이터 들어오는거 집어넣음
- 근데! 여러개라면 셋의 entry 중에서 선택
- Least-recently used(IRU) : 가장 오랫동안 사용하지 않은 엔트리로 선정
- Random 도 가능.. (높은 associative의 경우)
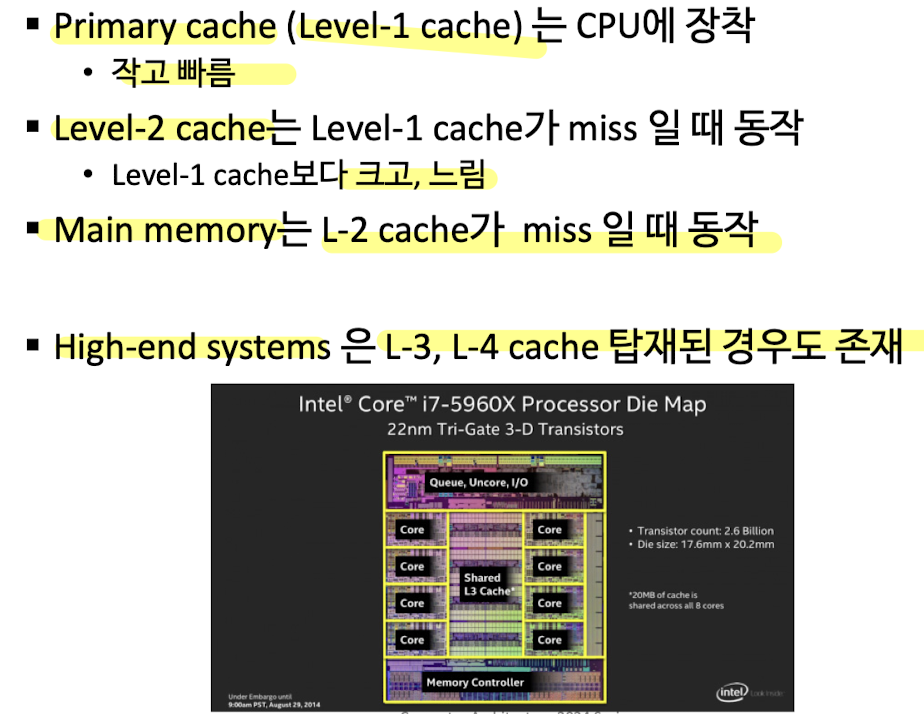
Multilevel Caches
'⚙️Computer System > 컴퓨터구조' 카테고리의 다른 글
| 🖥️ 컴퓨터구조 - Performance (수식) (0) | 2024.06.04 |
|---|---|
| 🖥️ 컴퓨터구조 - Matrix Multiplication & Virtual Memory(TLB) (0) | 2024.05.27 |
| 🖥️ 컴퓨터구조 - pipelining hazard 중 Forwarding 조건 & 동적 branch 예측 (0) | 2024.05.11 |
| 🖥️ 컴퓨터구조 - pipelined processor - 구조적 해결ㅊ책 이거 맞음? (0) | 2024.05.11 |
| 🖥️컴퓨터구조 - simple processor (0) | 2024.04.30 |




