코드네임 :
💿 자료구조 - Prim Algorithm 프림 알고리즘 본문
Greedy Algorithm
: 여러 개 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택
Prim Algorithm
Step1) 임의의 정점에서 가장 적은 비용으로 자신에게 이을 수 있는 정점을 선택 ( 비용 적은 걸로 이음)
Step2) 만들어진 '트리'에서 가장 적은 비용으로 트리에 이을 수 있는 정점을 선택 ( 현재 만들어진 트리 전체를 봐야함요 )
Step3) 반복하여 MST (정점을 모두 연결, cycle 없음) 만듦




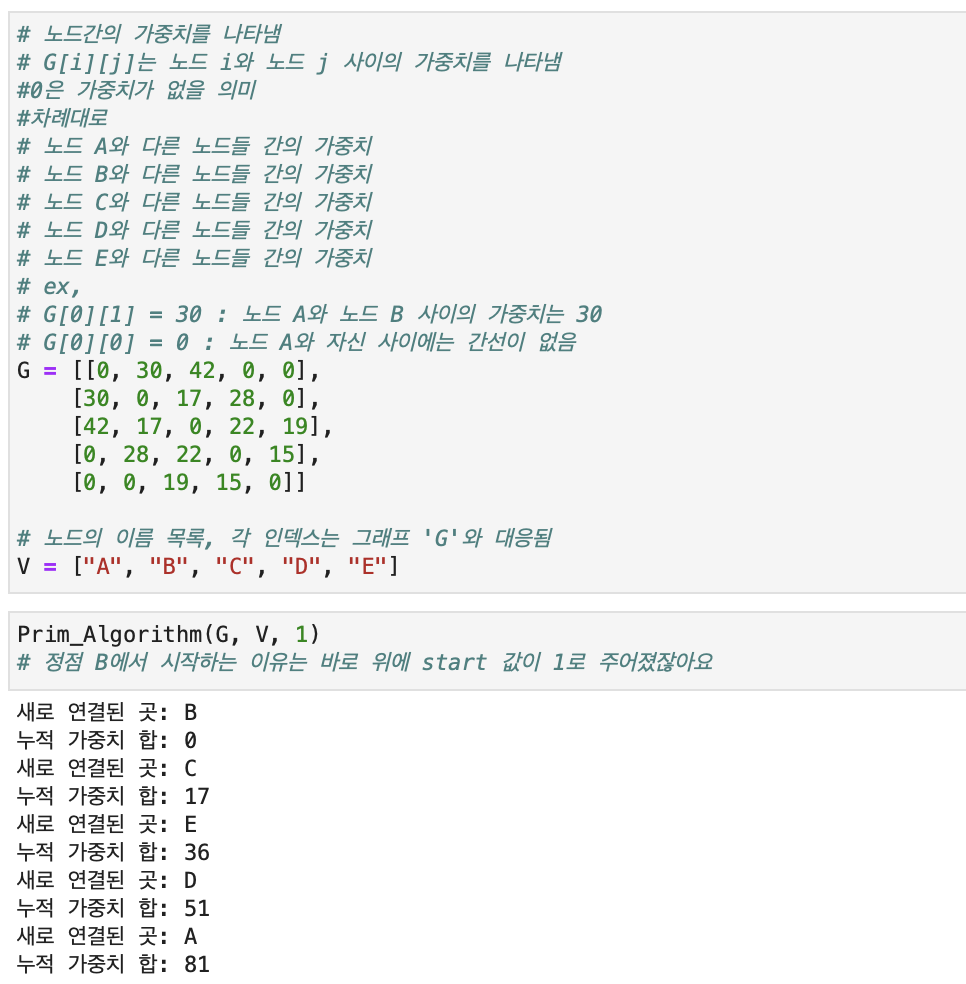
Prim Algorithm의 구현
- 아직 연결되지 않은 노드들에 대해서 연결 비용 업데이트
- 그중 최솟값을 취함
시간복잡도
정점의 개수를 V라 했을 때,
1) 하나의 임의의 정점을 고르고, 이와 연결되지 않은 정점들의 가중치 업데이트 : V-1번 수행
2) 그중 최솟값 찾기 : V-1번 비교 수행
3) 위 과정을 모든 정점 V에 대해서 수행
⬇️
v{(v-1)+(v-1)} = v(2v-2) = O(v^2)
성능향상
- 데이터 추가하면서 계속 최솟값 찾기
- 최솟값 찾기에 우선순위 큐 사용




⬇️
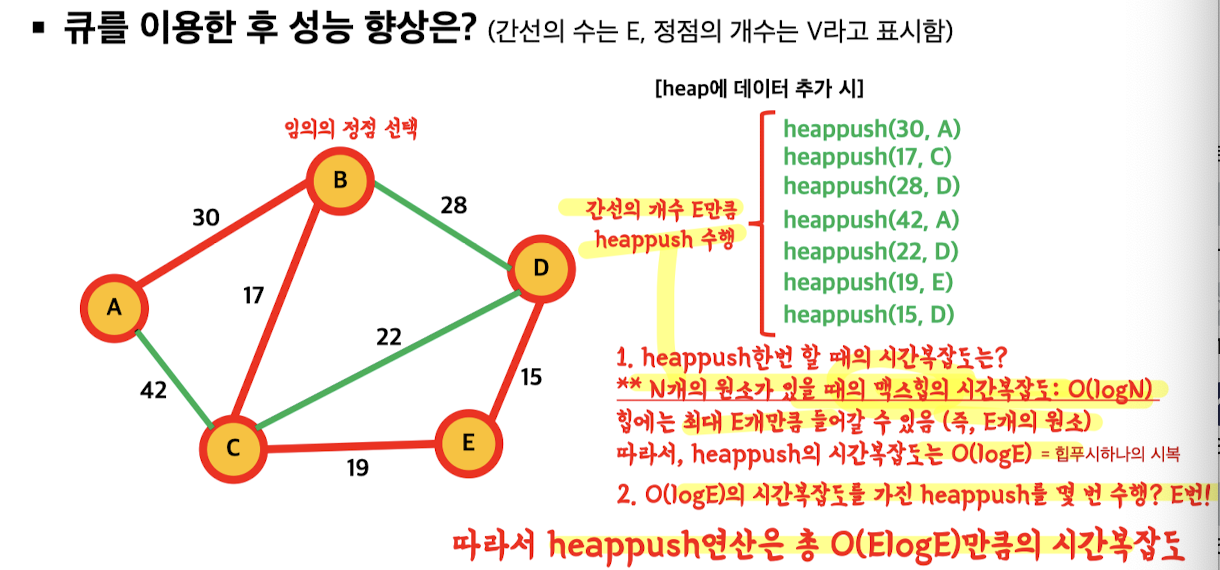
heappush :
1. heappush 한번 할때 시간복잡도 : O(logE)
( N개의 원소가 있을 때의 maxheap 의 시간 복잡도 : O(logN) )
( 힙에는 최대 E개의 원소가 들어갈 수 있음 )
( 따라서 heappush의 시간복잡도 = O(logE) )
2. O(logE)의 시간복잡도를 가진 heappush를 E번 수행할 떄 : O(ElogE)
( E번 * 1번의 시간복잡도)
heappop :
1. heappop 한번 할때 시간복잡도 : O(logE)
( N개의 원소가 있을 때의 maxheap 의 시간 복잡도 : O(logN) )
( 힙에는 최대 E개의 원소가 들어갈 수 있음 )
( 따라서 heappop의 시간복잡도 = O(logE) )
2. O(logE)의 시간복잡도를 가진 heappop를 E번 수행할 떄 : O(ElogE)
( E번 * 1번의 시간복잡도)

⬇️
성능이 향상된 프림 알고리즘의 총 시간복잡도 : O(ElogV)
O(ElogE + ElogE) = O(2ElogE) = O(ElogE)
이때, 간선의 수는 최대 V(V-1)/2개
즉, E <= V^2
(얘 위에것 처럼 v(v-1)(v-1) = v(2v-2) = O(v^2) 한거임)
(근데 시복이 아닌데 왜 이렇게 했냐고??)
(어짜피 시복에 대입할거자나)
따라서, O(ElogV^2) = O(2ElogV) = O(ElogV)
➡️ 개선되었다

https://github.com/codenameVien/DataStructure/blob/main/PrimAlgorithm.ipynb
DataStructure/PrimAlgorithm.ipynb at main · codenameVien/DataStructure
Contribute to codenameVien/DataStructure development by creating an account on GitHub.
github.com
'👩💻알고리즘 > 자료구조' 카테고리의 다른 글
| 💿 자료구조 - Dijkstra Algorithm 다익스트라 알고리즘 (0) | 2024.06.05 |
|---|---|
| 💿 자료구조 - Kruskal Algorithm 크루스칼 알고리즘 (0) | 2024.05.24 |
| 💿 자료구조 - 최소신장트리 MST (1) | 2024.05.23 |
| 💿자료구조 - Topological Sort 위상 정렬 (0) | 2024.05.16 |
| 💿자료구조 - BFS and DFS (너비 와 깊이 우선탐색) (1) | 2024.05.16 |




