코드네임 :
💿 자료구조 - 이진 트리 (와 그래프) 본문
선형 자료구조 - Linked List, Stack, Queue
비선형 자료구조 - Tree, Graph
[ Graph ]
연결되어 있는 대상(정점) 간의 관계를 표현하는 자료구조
- 정점(vertices)과 간선(edge)로 이루어짐

보행(Walk)
특정한 정점에서 다른 특정한 정점으로 갈때 거치는 정점과 간선의 나열
(그냥 모든 그래프)
닫힌 보행 (Closed Walk)
: 시작 정점과 종료 정점이 동일한 walk
A - B - C - D - E - C - B - A
열린 보행 (Open Walk)
: 시작 정점과 종로 정점이 다른 walk
A - B- C - D - E - D
경로 (Path)
: 같은 정점 및 간선이 중복되지 않은 walk
A - B - C - D - E
순환 (Cycle)
시작 정점과 종료정점이 동일한 path
닫힌 보행과 경로(path)의 조건을 모두 만족 (시작 정점과 종료 정점이 중복되는 것은 무시)
B - C - D - B
연결 그래프 (Connected Cycle)
: 모든 두 정점 사이에 경로(path)가 존재하는 그래프
[ Tree ]
1 . 주어진 그래프는 연결 그래프
2. 주어진 그래프는 순환(Cycle) 가지지 X
노드 (node)
- 부모와 자식 관계
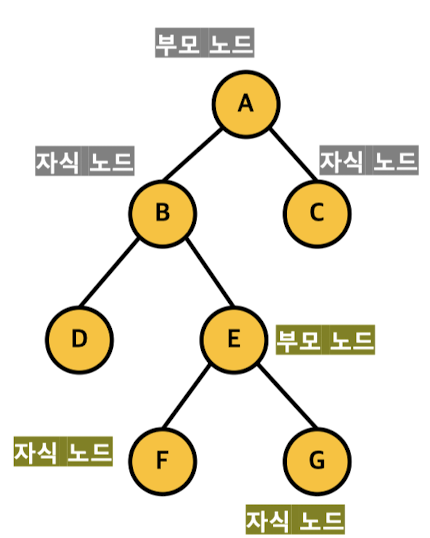
root 노드와 leaf 노드
root : 부모를 갖지 않는 노드 (즉 최상단 노드)
leaf : 자식을 갖지 않는 노드 (즉 최하단 노드)
- Leaf노드가 아닌 모든 노드를 ' 내부 노드 '라고 한다

깊이 (Depth)
: 자신을 제외한 조상 노드의 개수
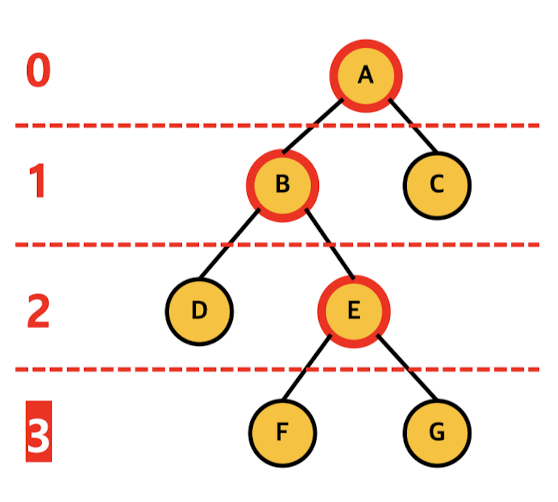
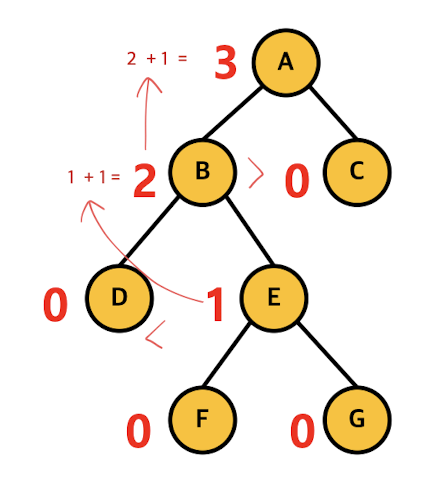
높이 (Height)
: 노드의 높이
: leaf 노드인 경우 0
: 내부 노드인 경우 해당 노드의 ' 자식의 높이 중 가장 높은 값 + 1 '
이진 트리 (Binary Tree)
모든 노드가 ' 최대 ' 2개의 자식 노드를 갖는 트리
(따라서 한줄짜리(자식노드가 전부 1개씩)도 이진 노드임)
포화 이진 트리 (Perfect Binary Tree)
트리의 각 레벨에 노드가 꽉 차 있는 이진 트리
< 조건 > 둘다 만족해야함
1. 모든 내부 노드의 자식이 2마리
2. 모든 Leaf 노드의 depth가 동일한 이진 트리

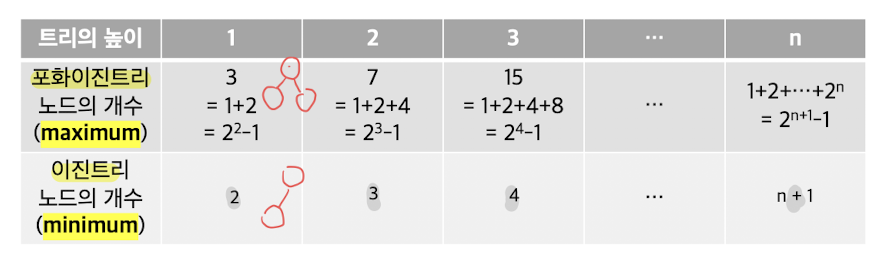
- 트리의 높이에 따라 노드의 개수가 정해져 있다
트리의 높이 : n
인 경우,
포화이진트리 노드 개수 : 2^(n+1) - 1
완전 이진 트리 (Complete Binary Tree)
트리의 최하단을 제외하고는 포화 이진 트리를 이루며, 최하단의 모든 노드는 좌측에 몰려있는 경우
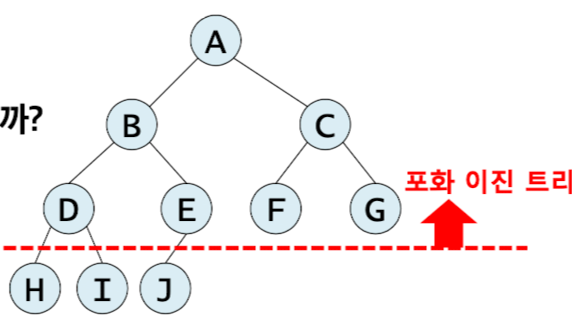
🙏
포화 이진 트리 : 그냥 다 꽉꽉! 들어찬 트리
완전 이진 트리 : 왼쪽부터 꽉꽉! 들어찬 트리
모든 포화 이진 트리는 완전 이진트리이다 (O)
모든 완전 이진 트리는 포화 이진 트리이다 (X)
🙏
[ 이진 트리의 성질 ]
노드의 개수가 n개이면 간선의 개수는 n-1
높이가 h라면 h+1 ~ 2^(h+1)-1 개의 노드를 가짐

[참고]
N개 노드의 이진트리 높이 : [log2(N+1)] - 1 ~ N
Q. 노드가 N개인 완전 이진 트리에 대한 설명으로 옳은 것은?
1. N이 짝수인 경우 포화 이진 트리일 수 없다 : ㅇㅇ (포이진은 높이에 따라 이진트리개수가 정해져 있음 + 홀수임)
2. 트리의 높이를 hN이라고 할 때, 노드 탐색 시 시간 복잡도는 O(hN) = log N이다 : ㅇㅇ
( 여기서 표현안되는데 hN에서 N은 작은 N 입니데,, h가 N에 영향을 받는다는 의미겟쬬 )
트리의 높이가 n일 때 완전 이진트리 노드의 개수는 2^n ~ 2^(n+1) -1 개
이진트리 노드 개수 N :
N = 2^n ~ N = 2^(n+1) -1
N+1 = 2^(n+1)
log2(N) = n ~ log2(N+1) = n+1
log2(N+1) -1 = n ( 노드 개수가 N일때 시간복잡도(= 트리의 높이) 는 log2(N) ~ log2(N+1) )
-> log2(N) = n( 시간복잡도는 쓸데 없는거 지우니께)
=> O(logN / log2) => 옆이랑 똑같음
= O(log N)
(시간복잡도는 쓸데 없는거 지우니께)

3. Leaf 노드의 수는 내부노드의 수와 항상 같거나 하나가 더 많다 : ㅇㅇ (아니 최하단 깊이 리프가 한개면 그거보다 깊이값 위에 있는거에도 리프가 있을거 아님!! 헷갈리지 말라노)
'👩💻알고리즘 > 자료구조' 카테고리의 다른 글
| 💿 자료구조 - Priority Queue 우선 순위 큐 (0) | 2024.04.12 |
|---|---|
| 💿 자료구조 - Heap (1) | 2024.04.12 |
| 💿 자료구조 - Deque 덱 (1) | 2024.04.11 |
| 💿 자료구조 - Queue 큐 (0) | 2024.04.05 |
| 💿 자료구조 - Stack 스텍 (0) | 2024.03.28 |




