코드네임 :
🖥️ 컴퓨터구조 진수 변환과 곱셈기/나눗셈기 본문
왜 10진수를 사용하지 않고 2진수를 사용할까요??
ㄴ 그거슨 2진수가 보관에 용이, 산술함수의 간단한 구현, 안정적으로 전송 이 가능하기 때문
N비트로 2의 N승개의 것들을 표현가능!!
2진수 0b 로 시작
8진수 0
16진수 0x
예.. 진수 변환법 다 까먹었네유..
⬇️ 진수 변환법 참고 블로-그
https://mingtrace.tistory.com/605

부호 없는 이진 정수
범위 : 0 ~ 2^n -1 (n은 bits)
< 2의 보수 >
부호 있는 정수 (음수)
- 0 이 하 나!
- 최신기계에서 거의 사용
~ x + 1 = - x ~
// 주어진 2진수의 모든 비트를 반전 (0을 1로, 1을 0으로) 후 , 1을 더함ex)
1000 0111 의 2의 보수
-> 0111 1000
-> 0111 1000 + 1 = 0111 1001
1000 1000 의 2의 보수
-> 0111 0111
-> 0111 0111 + 1 = 0111 1000
<Sign Extension 부호 확장> - 비트를 더 큰 저장공간으로 옮길 때
- w bits -> w+k bits
- sign(부호) 비트를 왼쪽으로 복제!!!
- 10진수 +2 : 0000 0010 -> 0000 0000 0000 0000
- 10진수 -2 : 1111 11111 -> 1111 1111 1111 1111
RISC - V
- {24bM[](7), M[R][rs1]+imm](7:0)}
: 24개의 비트는 원래 있던 7번비트(sign비트)를 갖다가 반복해서 집어넣었고, 7부터 0까지의 비트를 마지막에 집어넣었다.
< 비트 연산 >
1. & AND 연산 (0이 있으면 0 - 하나라도 False 면 False)
0000 1100
& 0001 1001
-----------
0000 1000
2. | OR연산 (1이 있으면 1 - 하나라도 True면 True)
0000 1100
| 0001 1001
-----------
0001 1101
3. ^ XOR 연산 (현암기 때.. 같은건 0으로 다른건 1로)
0000 1100
^ 0001 1001
-----------
0001 0101
4. 보수 (모든 비트를 역으로)
~ 0000 1100
-------------
1111 0011
<Shift>
[ 왼쪽 이동 : x << y ]
- 논리와 산술 이동이 똑같음 (즉, 굳이 log, arith 나눌 필요 X)
- 항상! 0으로 오른쪽을 채움
| 인수 x (양수) | 0110 0010 |
| <<3 | 0010 0000 |
| Log. >>2 | 0001 1000 |
| Arith. >> 2 | 0001 1000 |
[ 오른쪽 이동 : x >> y ]
- 논리와 산술 이동이 다름!!! ( 양수 인수는 ㄱㅊ으나 음수 인수일 때 문제 생길수 있어서 )
- 논리 이동 : 0으로 왼쪽을 채움
- 산술 이동 : 기존 인수의 MSB(부호비트)를 오른쪽에 복제함
| 인수 x (음수) | 1010 0010 |
| <<3 | 0001 0000 |
| Log. >> 2 | 0010 1000 |
| Arith. >> 2 | 1110 1000 |
< 오버플로우 >
[ 정수 덧셈 ]
1이면 올리기 (1+1 = 10 이런거.. 1+)
오버플로우는 양 + 음 인 경우 발생하지 않는다
양수끼리 더하면 결과 부호가 1
음수끼리 덜하면 결과 부호가 0
[정수 뺄셈]
2의 보수를 이용하여 덧셈으로 바꾸는 게 낫지 않을까요
오버플로우는 두 양끼리 또는 뚜 음끼리 뺼 때 발생하지 않은다
양수 - 음수 = 결과 부호 0
음수 - 양수 = 결과 부호 1
SIMD (single-instruction, multiple-data 하나의 명령으로 여러개의 얼굴)
오버플로우의 경우, 결과값은 표현할 수 있는 가장 큰 값)
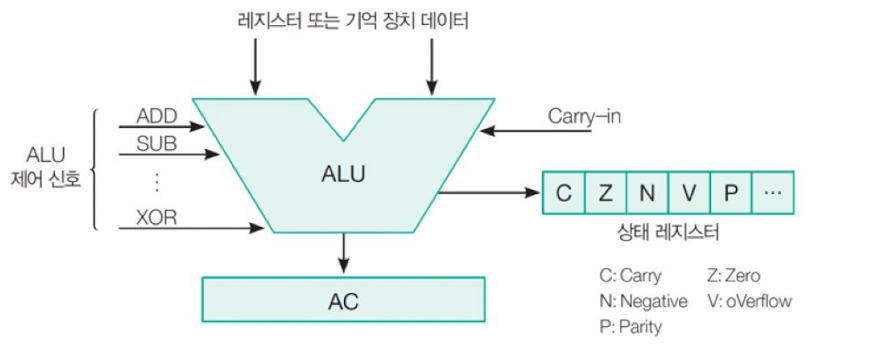
ALU (산술 논리 장치)
- 비트 단위의 산술연산(+,- 등) 또는 논리 연산(AND, OR, XOR)을 수행하는 장치
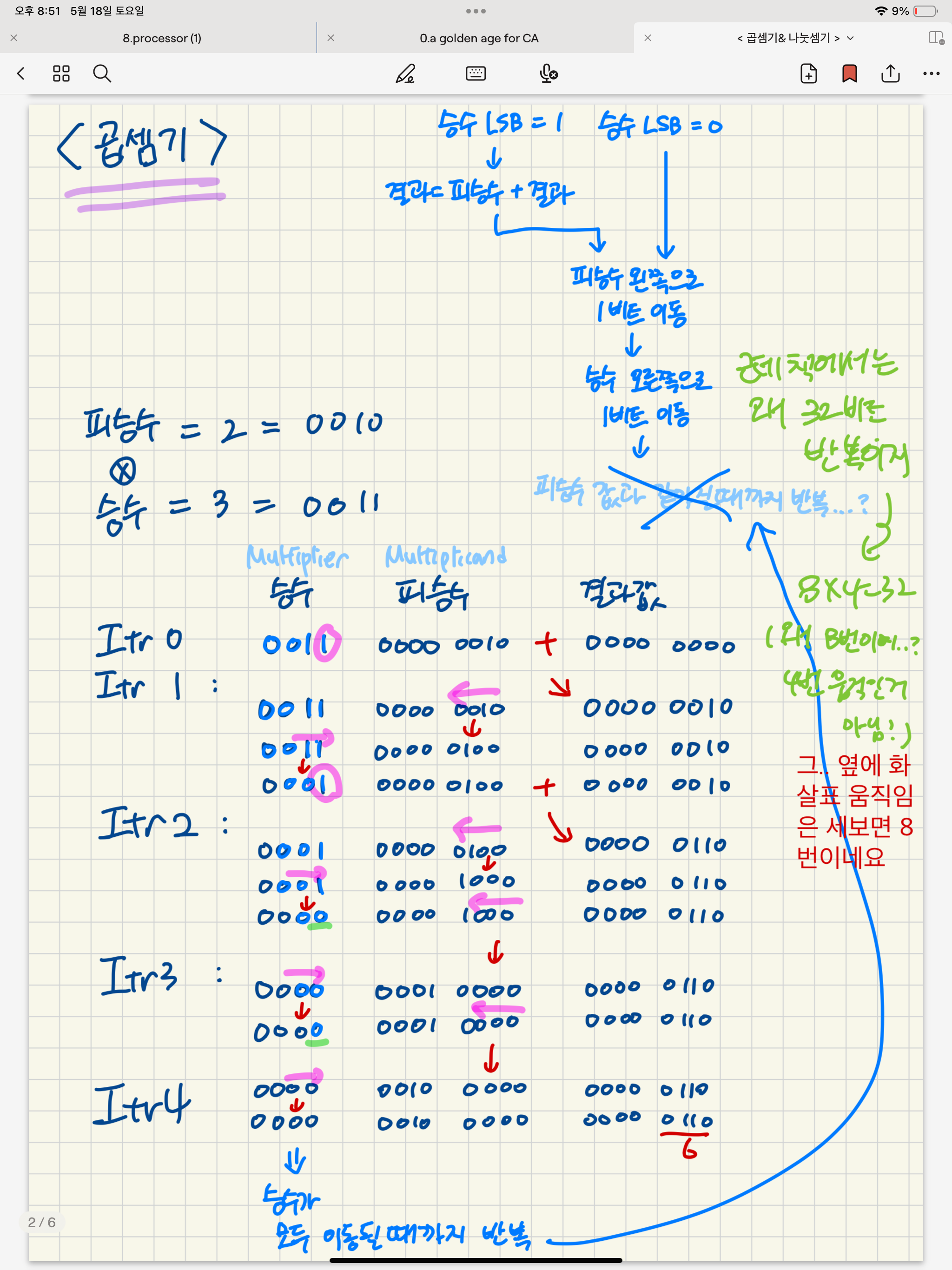
곱셈기

나눗셈기


곱셈기 나눗셈기 참고는
https://ttl-blog.tistory.com/1013
https://ttl-blog.tistory.com/1014
[컴퓨터 구조] 컴퓨터 연산[3] - 나눗셈
🧐 나눗셈 나눗셈은 다음과 같은 과정을 통해 계산됩니다. 나눗셈의 피연산자는 피제수(dividend)와 제수(divisor) 두 개이며, 몫(quotient) 과 나머지(remaunder) 두 개의 결과가 있습니다. 여기서 나머지
ttl-blog.tistory.com
'⚙️Computer System > 컴퓨터구조' 카테고리의 다른 글
| 🖥️컴퓨터구조 과제 2 📚 (0) | 2024.04.05 |
|---|---|
| 🖥️ 컴퓨터구조 RISC-V (0) | 2024.03.25 |
| 🖥️ 컴퓨터구조 Floating Points 부동소수점 (0) | 2024.03.19 |
| 🖥️ 컴퓨터 구조 과제1 📚 (0) | 2024.03.19 |
| 🖥️ 컴퓨터 구조 1주차 (0) | 2024.03.17 |


